1. Collection이란?
[ 배열과 컬렉션, 무엇이 다른가? ]
배열은 정적이다. 그에 비해 컬렉션은 동적이다. 이 말이 어려울 수 있기에 코드를 통해 쉽게 이해해보자.
우리가 배열을 생성할 때 어떻게 코드를 작성할까? 자바의 배열을 알고 있는 사람은 아래와 같이 배열을 생성할 것이다.
int[] arr = new int[5];
arr의 배열을 만들기 위해서는, 배열을 만드는 시점에 미리 5칸의 배열을 생성해야 한다.
즉, 배열이 생성되는 시점에 정적으로 배열 크기를 지정해줘야 한다는 단점이 존재한다는 것이다.
그렇다면 컬렉션은 어떻게 동적으로 배열을 생성할까? 이를 알아보기 위해 Collection을 상속받는 기본적인
List 자료구조를 직접 만들어보자. 이해가 목적이기에, 간단하게만 작성해보았다.
public class MyList {
private static final int DEFAULT_CAPACITY = 5;
private Object[] elementData;
private int size = 0;
public MyArrayListV2() {
elementData = new Object[DEFAULT_CAPACITY];
}
public MyArrayListV2(int initialCapacity) {
elementData = new Object[initialCapacity];
}
public int size() {
return size;
}
public void add(Object e) {
if (size == elementData.length) {
grow();
}
elementData[size] = e;
size++;
}
private void grow() {
int oldCapacity = elementData.length;
int newCapacity = oldCapacity * 2;
elementData = Arrays.copyOf(elementData, newCapacity);
}
해당 코드를 보면 이해가 쉽다.
컬렉션 또한 배열 기반이기에, 초반에 배열 크기를 정해줘야 한다. 값을 하나씩 넣을때마다, 배열의 size를 증가시켜
알맞는 위치에 값이 들어가도록 설정한다. 배열의 크기가 가득찰 경우, 기존 수용량 * 2 후, 기존 배열을 복사해 새롭게
저장한다.
그러면 배열 대신에 컬렉션을 사용하면 어떤 이점이 있을까?
- List, Set, Map, Queue와 같은 자료구조를 쉽게 사용할 수 있다.
- 동적으로 배열을 생성할 수 있다.
- Collection이 제공해주는 메서드를 간편히 사용할 수 있다. ex) add(), size(), remove(), contains() ...
Collection을 사용하기 위해서는, 자바에서 제공하는 Collection에 대해 이해해야 한다. 이 글을 쓰는 목적이다.
아래 글을 통해 Collection이 제공해주는 자료구조들에 대해 천천히 알아보자.
모든 자료구조를 다루진 않을 것이고, 제목에 맞게 코딩 테스트를 풀기 위한 자료구조 에 대해서만 다룰 것이다.
2. List
리스트를 구현하기 위해서는 여러 가지 구현체가 있지만, 이 글에서는 ArrayList와 LinkedList의 특징에 대해서만 살펴보려고 한다.
[ ArrayList ]
가장 많이 사용하는 리스트의 구현체이다. ArrayList의 특징은 어떤 것이 있을까?
List<Integer> arr = new ArrayList<>();
arr 컬렉션을 하나 만들었다. 내부 코드를 살펴보았을 때,
public class ArrayList<E> extends AbstractList<E>
implements List<E>, RandomAccess, Cloneable, java.io.Serializable
{
@java.io.Serial
private static final long serialVersionUID = 8683452581122892189L;
/**
* Default initial capacity.
*/
private static final int DEFAULT_CAPACITY = 10;
DEFAULT_CAPACITY = 10 이라는 것을 알 수 있다. 하지만 그림으로 설명할 예정인데, 10칸은 너무 많기 때문에
내 맘대로 5칸으로 그려서 설명하려고 한다.
- 삽입의 경우
3가지의 경우로 나눠서 설명할 수 있다. 1) 맨 앞에 삽입하는 경우, 2) 중간에 삽입하는 경우, 3) 맨 뒤에 삽입하는 경우 에 대해 살펴보자.
1) 맨 앞에 삽입하는 경우
ArrayList에 값을 삽입하는 경우, 첫 번째 인덱스의 공간이 비어있어야한다. 즉, 배열 안에 있는 값들을 한 칸씩 뒤로 밀어야한다는 소리다. 그림으로 살펴보자.

현재 index 0, 1, 2 에 값이 들어있는 상태이고, 맨 앞에 4를 추가하기 위해서는 1, 2, 3을 한 칸씩 뒤로 밀어야 한다.

ArrayList에서 맨 앞에 값을 삽입하는 경우, 배열의 크기가 5라면 5번, 크기가 100이라면 100번 요소를 이동해야
하기 때문에, O(n)의 시간 복잡도를 가지는 것을 알 수 있다.
2) 중간에 삽입하는 경우

이 경우 또한 맨 앞에 삽입할 경우와 마찬가지로 삽입할 index 2 의 자리를 마련하기 위해 2,3을 한 칸씩 뒤로 밀어야한다.

해당 경우는 O(n/2) 이기 때문에, 중간에 삽입하는 경우 또한 O(n) 의 시간복잡도를 가지는 것을 알 수 있다.
3) 맨 뒤에 삽입하는 경우

맨 앞의 삽입, 중간의 삽입과 다르게, 기존의 값을 뒤로 미루지 않아도 된다.

그렇기에 해당 작업은 index의 크기를 찾는, O(1) 시간복잡도를 가진다.
- 삭제의 경우
1) 맨 앞을 삭제하는 경우

맨 앞의 index를 삭제하면 어떤 일이 일어날까? 해당 인덱스가 비어있을까?
아니다. 비어있는 인덱스는 존재해서는 안 된다. 그렇기 때문에 2,3을 한 칸씩 앞으로 당겨와야 한다.
삽입과 마찬가지다. 다만, 삭제는 한 칸 미루는 것이 아닌, 한 칸 당겨온다.
그리고 Collection은 동적이기 때문에 삭제가 이루어졌을 때 메모리를 최적화 하기 위해 배열의 크기가 줄어드는 작업 또한 이뤄진다. 그렇기에 O(n) 시간복잡도를 가진다.
2) 중간 값을 삭제하는 경우
삽입 예제를 이해하고, 앞의 값 삭제를 이해했다면 중간 값 삭제 또한 이해했을 것이라 생각한다.
O(n) 시간복잡도를 가진다.
3) 마지막 값을 삭제하는 경우
삽입과 마찬가지다. 삭제 또한 한 칸 당겨올 필요가 없기에 O(1)의 시간복잡도를 가진다.
ArrayList의 시간복잡도 정리
- 맨 앞 삽입, 삭제: O(n)
- 중간 삽입, 삭제: O(n)
- 맨 뒤 삽입, 삭제 O(1)
[ LinkedList ]
LinkedList를 이해하기 위해선 우선 Node를이해해야 한다.
public class Node {
private Object item;
private Node next;
public Node (Object item){
this.item = item;
}
노드는 값을 담는 item, 그리고 다음 노드의 참조값을 담는 next로 이루어진다. 말로 하면 이해가 안 될 수 있으니, 그림으로 살펴보자. 해당 객체를 그려보면 아래와 같은 그림이 그려진다.

이제 해당 객체를 생성해보자.
Node first = new Node("A");
객체를 생성한 후의 모습은 다음과 같다.

first.next = new Node("B");
예를 들어, 첫 번째 노드의 아이템 값을 찾고 싶다면 first.item과 같이 찾을 수 있을 것이고,
두 번째 노드의 아이템 값을 찾고싶다면 first.next.item 과 같이 찾을 수 있다.
해당 구조는 각각의 Node들이 참조를 통해 연결(Link) 되어 있다. 이 구조를 사용해 List로 구현한 것이 바로 LinkedList다.
LinkedList의 특징
1) 값을 조회하는 경우 - O(n)
index를 조회할 때 LinkedList는 O(n)의 시간복잡도가 소요된다. 왜그럴까?
기존의 배열 및 ArrayList는 특정 인덱스 값을 찾는데에 O(1)이 소요되었다. 그런데 왜 LinkedList는 O(n)의
시간복잡도를 가지는걸까?
-> 연결리스트의 노드들은 배열이 아니다. 단지 다음 노드에 대한 참조가 있을 뿐이다.
따라서 index 3을 찾기 위해서는 첫번째 노드 ~ 3번째 index까지 3번 이동해야하고, n이면 n번 이동해야한다.
그렇기에 index 조회에서 O(n)의 시간복잡도가 소요된다.
2) 값을 추가하는 경우 - O(n)
조회와 마찬가지다. List에서 add() 메서드를 통해 값을 추가하는 경우, 마지막에 데이터가 추가된다.
ArrayList, 배열의 경우 O(1) 시간에 마지막 인덱스를 찾을 수 있지만, LinkedList에서는 마지막 인덱스를 찾는데 O(n) 시간이 소요된다. 그렇기에 값을 추가하는 경우 또한 O(n)의 시간복잡도를 가진다.
3) 맨 앞에 삽입, 삭제하는 경우 - O(1)
기존 ArrayList를 생각해보면, 리스트의 맨 앞에 값을 추가할 경우 맨 처음 index 공간을 마련하기 위해 한 칸씩 뒤로 미뤄야하는 상황이 발생했었다. LinkedList의 경우, 상황이 다르다. 그림으로 살펴보자.

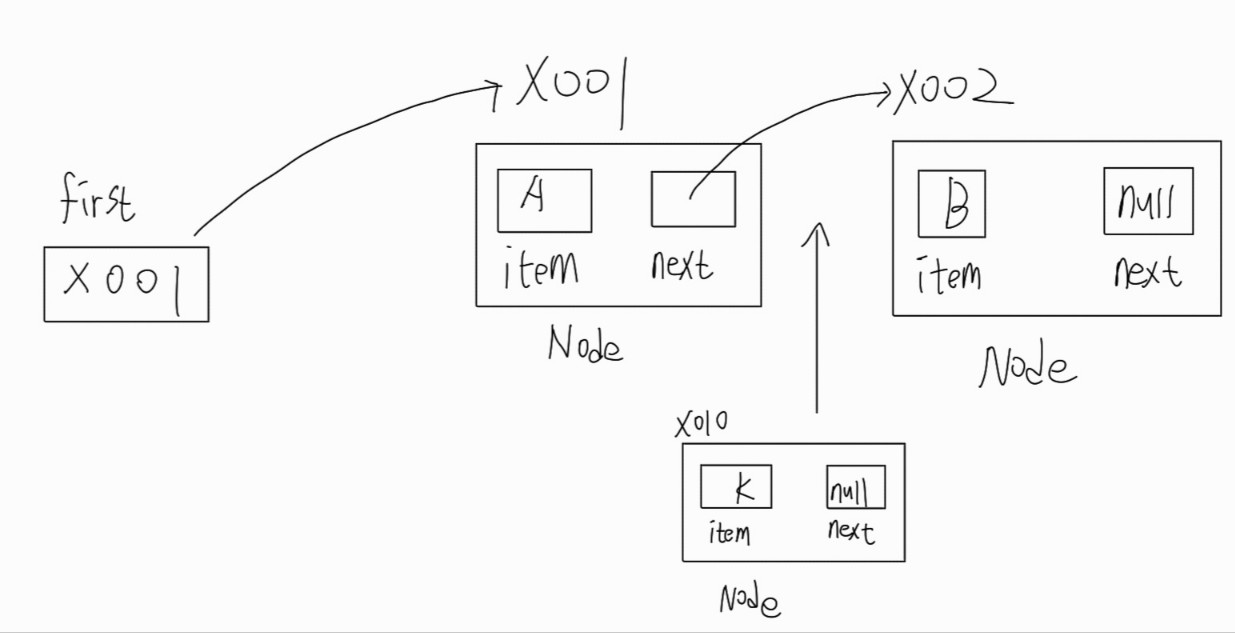
item값이 k인 Node를 맨 처음에 삽입하려고 한다. 어떻게 하면 될까?
first의 참조값을 x010으로 바꾸고, x010의 next 값을 x001의 참조값으로 바꿔주면 되지 않을까?
글로 하면 이해가 잘 안 될수도 있어 다시 한 번 그림을 통해 살펴보자.

first 의 참조값을 x010으로 바꿨고, x010의 next 값을 x 001로 설정했다. 아주 자연스럽게 맨 첫번째 값에
item값이 k인 노드를 삽입할 수 있었다.
해당 작업에서는 index를 찾는 작업 또한 필요없다. 그저, 참조값만 연결해주면 된다. 또한 실제로 index 값이 정해진 것이 아닌, 첫번째 연결된 노드를 index 0, 그 다음으로 연결된 노드를 index 1로 가정할 뿐이다. 그렇기에 ArrayList 처럼 배열을 한 칸씩 미루는 작업 또한 필요없다. 그렇기에 해당 작업은 상수시간 즉, O(1) 의 시간복잡도를 가진다. 맨 앞 삭제 또한 마찬가지로 참조값을 조정하면 되고 한 칸씩 당기는 작업 또한 필요없기에 동일하게 O(1)의 시간복잡도를 가진다.
3) 중간에 삽입, 삭제하는 경우 - O(n)
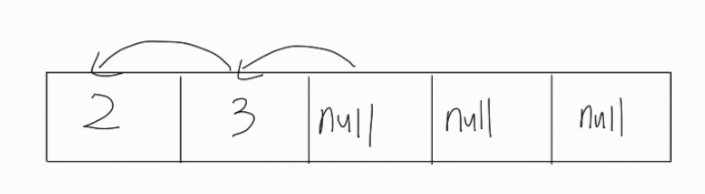
리스트의 중간에 값을 추가하는 경우다. 맨 앞 삽입과 비슷해보인다. x001의 참조값을 x010으로 변경하고, x010의 참조값을 x002와 연결시켜주면 자연스럽게 삽입이 될 것 같다. 이 과정은 O(1) 시간이 소요되지만, index를 찾는 시점에서 이미 O(n) 시간복잡도를 가진다.

그림으로 보면 이해가 수월할 것이다. 흐름이 비슷한데, 참조값 변경만 해주면 된다. 삭제 또한 마찬가지다.
3. ArrayList vs LinkedList 시간복잡도 비교
| 기능 | ArrayList | LinkedList |
| 인덱스 조회 | O(1) | O(n) |
| 맨 앞 삽입(삭제) | O(n) | O(1) |
| 맨 뒤 삽입(삭제) | O(1) | O(n) |
정리하자면 다음과 같은 표를 도출할 수 있다.
하지만 여기서 끝이 아니다. 자바에서는 LinkedList를 단방향 리스트가 아닌, 양방향 리스트로 사용한다.
next만 있는게 아닌, prev또한 존재해 이전으로도 이동할 수 있다는 말이다.

또한 마지막 노드에 대한 참조 또한 제공한다.
즉, 첫 번째 삽입과 마찬가지로 마지막에 데이터를 삽입할 때에도 O(1) 를 가질 수 있다.
그렇기에 자바에서 LinkedList를 사용한다면, 양방향 리스트 + 마지막 노드의 참조를 제공해주기 때문에
아래와 같이 표를 수정할 수 있다.
| 기능 | ArrayList | LinkedList |
| 인덱스 조회 | O(1) | O(n) |
| 맨 앞 삽입(삭제) | O(n) | O(1) |
| 맨 뒤 삽입(삭제) | O(1) | O(1) |
이번 포스팅에서는 Collection, 그 중 List에 대해서 알아봤다.
다음 글에서는 Map에 대해 알아보자.
'java' 카테고리의 다른 글
| Thread(2) - 스레드의 상태 (6) | 2025.01.15 |
|---|---|
| Thread(1) - java의 메모리 구조, 프로세스의 메모리 구조 (4) | 2025.01.14 |
| Java 컬렉션 정리 for 코딩테스트 - Queue (9) | 2024.12.25 |
| Java 컬렉션 정리 for 코딩테스트 - Map (7) | 2024.12.23 |
| Java 컬렉션 정리 for 코딩테스트 - Set (1) | 2024.12.22 |



